2022年9月25日模試

記事を読んでみて参考になったら、よろしければ、こちらか最後のリンクから応援クリックいただけると励みになります！
にほんブログ村

日能研の模試の特徴である、偏差値なしの成績表

先日、日能研で受けた全国テストの結果が帰ってきたことを紹介しました。

突然ですが、小学校2年生と小学校3年生の日能研の全国テストで見ることができる結果は、以下となっています。

• 受験者数
• 算数の点数、平均点、順位
• 国語の点数、平均点、順位
• 2教科の点数、平均点、順位

中学受験の模試でおなじみの「偏差値が無い」ことが特徴的ですね。同じ学年でも、四谷大塚の全国統一小学生テストや早稲田アカデミーのチャレンジテストでは偏差値が出力されます。ちなみに、後で知りましたが、日能研本科生が受ける「育成テスト」でも、成績表には偏差値が出力されないそうです。

「低学年のときから偏差値を気にすることに意味はない」、と言われていると思います。受験者数が必ずしも多くなかったり、4年生から塾通いが始まると習うことも多くなるため簡単に下がったり上がったりするためと理解しています。同様の理由で4年生や5年生前半の偏差値も当てにならないという話も見聞きしますね。

とはいえ、せっかく模試を受けるのだから、相対的な立ち位置が全く気にならない人は少ないように思います。順位が出るからある程度わかるというのも事実ではありますが、日能研の全国テスト、早稲田アカデミーのチャレンジテスト、四谷大塚の全国統一小学生テストで、受験者数も問題の内容も大きく変わるため、並列の比較はなかなか難しいところです。

そこで、「順位%」を使うことを考えます。自分の順位を受験者数全体の位置で把握すれば、相対的な位置がわかりますね。単純に、「（順位÷受験者数）×100」でわかります。でも、わざわざこんな計算をして成績をモニタリングする人は普通はいないと思います。成績の推移を見るなら、やはり「偏差値」の推移ですよね。

そうすると、成績の推移を知りたくても、「日能研の全国テストではデータが欠失してしまう」という課題が出てきます。せっかく受験しているのですから、なんとか偏差値に換算して、わが子の成績推移のデータに加えたいものです。勉強が本格的になった日能研本科生にとっては、育成テストも同様かと思います。

ということで、多少無理矢理感はあるのですが、わたしは「娘の模試での順位から偏差値を計算して、日能研の全国テストを他の模試と並べてデータの推移見る」ことができるようにしています。

偏差値の出ない日能研の全国テストで偏差値を計算する方法

結論だけ知りたい方も多いと思いますが、ここでは、理屈も含めて、日能研の全国テストで順位を偏差値に換算する方法を紹介いたします。

なお、同じく偏差値が出ない、日能研本科生が受験することになっている「育成テスト」でも、この計算方法はもちろん使うことができますが、そちらにより焦点を当てた偏差値計算については、計算式は同じではありますが、以下で紹介しています（3月始めごろ公開予定です）。

記事を読んでみて参考になったら、よろしければ、こちらか最後のリンクから応援クリックいただけると励みになります！
にほんブログ村

 

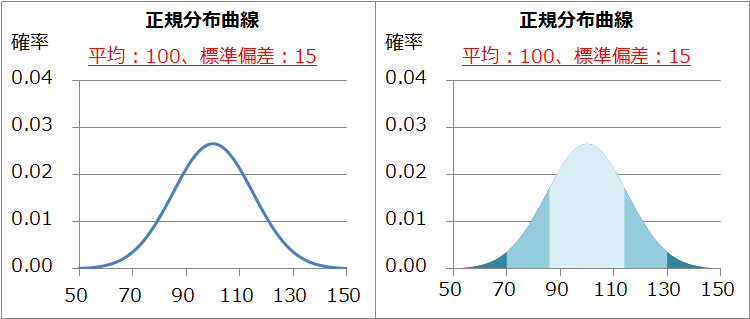
上の図は、平均点が100点で標準偏差が15点だった場合の正規分布曲線です。150点満点の模試だと、だいたい、こんな感じの分布になると思います。右側のグラフで塗りつぶされている部分からは、含まれる割合を読み取ることができます。偏差値の仕組みでご存じの方も多いかもしれませんが、

• 薄い青：平均値±標準偏差、全体の約68.3%が含まれる
• 普通青：平均値±2×標準偏差、全体の約95.5%が含まれる
• 濃い青：平均値±3×標準偏差、全体の約99.7%が含まれる

という仕組みになっています。平均値が異なれば分布が左右に移動しますし、標準偏差が異なれば分布が狭くなったり広がったりするということになります。そうすると、異なる分布間での比較ができなくなってしまいます。たとえば科目が異なると比較できなくなるということですね。これは困ります。

 

 

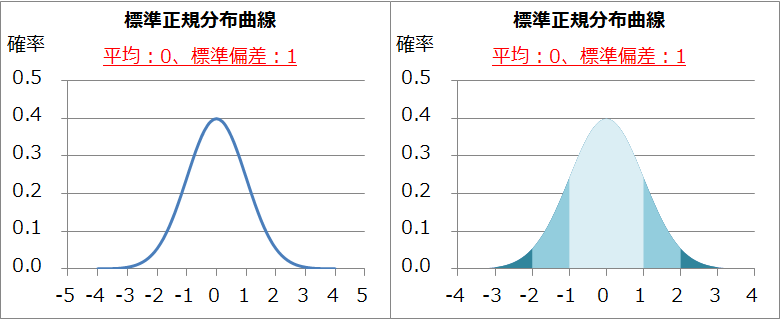
でも、これは、一般的に、「データ（テストでは点数）から平均値を引いて標準偏差で割る」という、「標準化」という操作をすることで解決します。標準化は、「基準化」や「正規化」と呼ばれることもありますね。

上の図は、標準正規分布曲線です。標準化は、普通は正規分布を標準正規分布に変換するときに利用されます。

よく見ると、横軸がどこかで見たことがある図に近くなっているように思います。

 

 

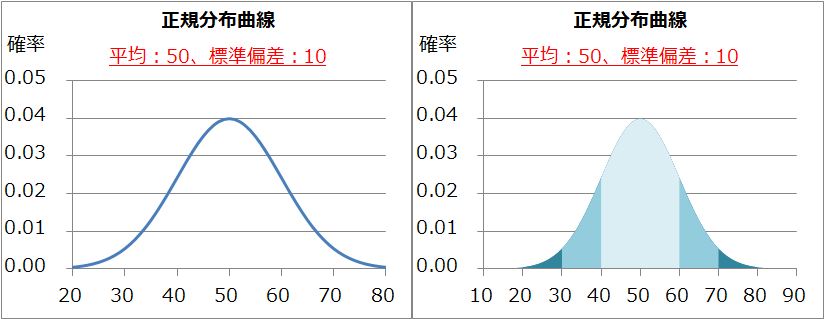
そして、こちらが偏差値の考え方ですね。標準正規分布とくらべると、平均と標準偏差が異なる以外は、普通はほぼ重なってきます。

よく見ると、確率の部分は、3つの図でもほとんどかわりません。そのため、「テストの点数から確率（つまり順位%）を求め、確率から偏差値を求める」事ができるということになります。

実際には、テストの点数は完全に正規分布に従っているわけではないと思います。しかしながら、受験者数の数が多いことや、大手塾は受験者層をきちんと見ていて、できるできないがうまく正規分布に従ってわかれるように問題を作成している（はず）ことから、気にしないことにします。そもそも、とりあえず何でもいいから偏差値を出したいという趣旨ですし。

ここから、エクセルでの偏差値計算の操作に入ります。

まずは、受験者と順位から、順位%を計算します。順位が高いほどゼロに近づき、順位が低いほど100に近づくように計算します。反対でも計算できますが、しばしば「上位10%」のような言い方をしますので、このほうがイメージに近いと思います。

• 順位%＝順位÷受験者数

上記の式は、0～1の小数で表すことを想定し、「×100」はしていません。わかりやすいからということで百分率にしたいときには「×100」しますが、その場合、後述の関数で引用するときに「÷100」が必要となります。

そして、普通は誰も使わないと思われる、エクセルの関数「NORM.S.INV」に登場いただきます。この「NORM.S.INV」関数は、「標準正規分布の累積分布関数の逆関数を返す」という、まったくもって意味不明なことを計算してくれる関数です。なお、エクセルのバージョンによっては「NORMSINV」と、ピリオドがいらないようですのでご注意ください。

「NORM.S.INV」関数は、「NORM.S.INV(確率)」という形で使います。そして、ここで、(確率)に「順位%」を百分率ではなく、0から1の範囲で入力します。

• 確率：上で計算した順位%

前述の通り、順位%は下から数えるか上から数えるかができますが、今回は順位が高いほどゼロになるように計算していますので、「NORM.S.INV(確率)」で出てきた値に「-1」をかけるという操作をします。つまり、

-1×「NORM.S.INV(“順位%")」

ですね。もしも、順位%の計算に「×100」を入れているようであれば、

-1×「NORM.S.INV(“順位%"/100)」

となります。

そして、これに以下を加味します。

• 平均：50（偏差値の平均値は50です）
• 標準偏差：10（偏差値の標準偏差は10です）

これで数式が完成します。エクセルにコピペできる計算式は後述しますが、数式は、

-1×「NORM.S.INV(“0から1の順位%")」×10＋50

または、

-1×「NORM.S.INV(“百分率の順位%"/100)」×10＋50

となります。

あるいは、「順位%」など邪魔という場合には、

-1×「NORM.S.INV(“順位"／"受験者数")」×10＋50

を使います。

コピペできる計算式、エクセルシート配布、順位と偏差値の換算表

これで、あくまでテストの点数の分布が正規分布に従うと仮定した場合ですが、順位を偏差値に換算することができるようになりました。

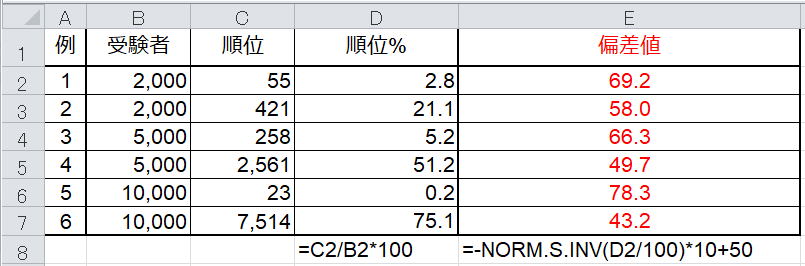
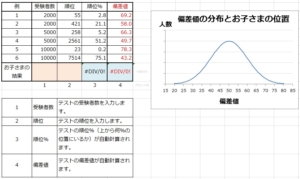
上記は、適当に数値を仮定した場合の計算例です。例1（2行目）の計算式は以下となっていますので、コピペして参照セルを変えればすぐに偏差値を計算できるかと思います。

受験者数（セルB2）

順位（セルC2）

順位%（セルD2）：=C2/B2*100

偏差値（セルE2）：=-NORM.S.INV(D2/100)*10+50

または、「順位%」なしで直接計算する場合には、

偏差値（セルE2）：=-NORM.S.INV(C2/B2)*10+50

最後のコピペできる数式だけ先に書けよと言われそうではありますが、これで順位から偏差値を計算することができました。

計算式ではなくエクセルシートをご希望の方向けに、「日能研の育成テスト・全国テストで偏差値を計算するシート」を、以下からダウンロードできるようにしています（二次配布はどうぞご容赦ください）。

日能研の育成テスト・全国テストで偏差値を計算するシート.xlsx
（Microsoft Defenderでスキャン済みです。）
ダウンロードいただきましたら、よろしければ応援クリックいただけると励みになります！

にほんブログ村

以下は、エクセルにコピーすることやダウンロードすることすら面倒という方のため、上位何%にあたるかの「順位%」と「偏差値」の換算表となります。

順位％	偏差値	偏差値（整数）		順位％	偏差値	偏差値（整数）		順位％	偏差値	偏差値（整数）
1	73.3	73		12	61.7	62		45	51.3	51
2	70.5	71		14	60.8	61		50	50.0	50
3	68.8	69		16	59.9	60		55	48.7	49
4	67.5	68		18	59.2	59		60	47.5	47
5	66.4	66		20	58.4	58		65	46.1	46
6	65.5	66		22	57.7	58		70	44.8	45
7	64.8	65		24	57.1	57		75	43.3	43
8	64.1	64		26	56.4	56		80	41.6	42
9	63.4	63		28	55.8	56		85	39.6	40
10	62.8	63		30	55.2	55		90	37.2	37
				35	53.9	54		95	33.6	34
				40	52.5	53

この「順位を偏差値に換算する方法」は、低学年でも偏差値をモニタリングした方がいいとか、そのようなことを言う意図はまったくなく、正確性は犠牲にしてでもとにかく偏差値を知りたいとか、エクセルでまとめたときに日能研の全国テストだけ偏差値のセルが空白で気持ち悪い・偏差値が欠失して推移が確認できないのをなんとかしたい、という方がいるかも知れないと思って紹介いたしました。みなさまのご参考になれば幸いです。

参考になるブログがたくさんあります！応援よろしくお願いします！
　⇨　中学受験を目指すブログへ
　⇨　2024年受験の参考になるブログへ
　⇨　早稲アカ仲間のブログへ

Twitterで娘への日々の小さなサポートを紹介し始めました。
Follow @zeropapa_jukenTweets by zeropapa_juken

おわりに

娘が中学受験で結果を出せるかどうかはわかりませんし、今、私が考えていること、やっていることが結果につながる自信があるわけでもなく、正直なところ、試行錯誤しているのが現状です。しかしながら、私と娘は小学2年生の半ばから中学受験を意識した勉強を開始し、新4年2月からの通塾開始までに、大手塾から以下のお誘いを受けた事実があるため、低学年時の勉強についてはある程度うまく進めることができたと言ってよいのかなと思っています。

・四谷大塚の全国統一小学生テストへの決勝招待（1回）
・日能研の全国テストと学ぶチカラテストで小4からのTMクラスへの招待（3回）、および、4年生1年間の奨学生制度（授業料および教材料等全額免除）のスカラシップ資格
・早稲田アカデミーのキッズチャレンジテストおよび冬季学力診断テストで半年の授業料免除の特待（3回）

私達は幼児教育もまるで考えず、中学受験を意識したものの、経験もなく何をやればいいかわからない状態からの始まりでした。同じような状況の親御さんたちにとって、何らかの参考になればと思っていますので、応援をどうぞよろしくお願いいたします。

[linkrank]

参考までに、娘の小学1年生から3年生までの成績は、小学1年生では5回の模試の2教科で平均偏差値59.8（最低50.8）から、小学2年生では9回の平均偏差値70.3（最低62.5）、小学3年生では8回の模試の2教科で平均偏差値71.3（最低68.6）となっています。

以下は、参考記事です。

以下のリンクから「模試」カテゴリの他の記事を探せます。