2022年11月16日模試,情報

記事を読んでみて参考になったら、よろしければ、こちらか最後のリンクから応援クリックいただけると励みになります！
にほんブログ村

日能研の模試の特徴？偏差値を出してもらえない

これまでに何度か書いたような記憶がありますが、私の職場の同僚のお子さんの中学受験率がとても高い印象を持っています。住んでいる地域も、学年によってばらつきがあるらしい話は聞きますが、それほど低いわけでもないようです。でも、その、住んでいる地域の子どもたちの中学受験率よりは、職場の子どもたちの中学受験率の方が明らかに高いように見受けられます。

その中には、もちろん日能研に通われているお子さんも少なくありません。

私達の場合、新4年生からの早稲田アカデミーへの通塾が始まるまで、娘はこれまで何度も日能研の無料模試（全国テスト、学ぶチカラテスト）を受けてきました。その中で、四谷大塚の全国統一小学生テストや早稲田アカデミーのチャレンジテストとはまた異なったタイプの問題だったこともあり、特に国語については、娘の国語の勉強をすすめる上でいろいろな気づきを得ることができました。私にとって、日能研の模試は、言わば、国語の学習方針を決めるための指針となったテストでもありました。とても感謝しています。

その日能研のテストですが、親の立場として少し困るのが、模試の結果として「順位は出るものの、偏差値がでない」ことでした。

低学年の偏差値などあてにならないというのが中学受験の世界の常識なようなのですが、それはそれとして、エクセルで管理しようとした場合、他の模試と横並びさせてもデータが欠失してしまって、比較したりグラフを描くことができないというのが、私にとっては困ったところでした。

それを何とかするため、順位から偏差値を計算する方法を、以前、以下のリンク先の記事で紹介いたしました。ちょっと無駄にマニアックですが、きちんと解説を用意したので、安心してお使いいただけると思います。

さて、実は日能研では「育成テスト」というテストがあるという話を同僚から聞きました。聞いた限りだと、早稲田アカデミーで言うところのカリキュラムテストのような位置づけと思います。

「全国テスト」や「学ぶチカラテスト」と同様に、この「育成テスト」もまた、偏差値が出ないという試験だそうです。それを聞いて、受験者数と順位が分かれば簡単に計算できることを同僚に教えたら、とても喜ばれました。この計算は、実は難しい話ではないのですが、意外と知られていなそうなので、改めて紹介したいと思います。

なお、「この計算でなぜ順位を偏差値に変換できるか？」という計算の原理については、上記のリンクから閲覧できますので、以前紹介した記事をご参考にしていただければと思います。

偏差値の出ない日能研の育成テストで偏差値を計算する方法

さて、ここから本題である、育成テストで偏差値を計算する方法です。

同僚に聞いた話によると、育成テストでは、以下の結果だけを知ることができるようです。

点数：国語、算数、理科、社会、2科（国算）、3科（国算理）、4科（国算理社）
平均点：国語、算数、理科、社会、2科、3科、4科
10段階の評価：国語、算数、理科、社会、2科、3科、4科
総合順位：2科、3科、4科
男女別順位：2科、3科、4科
受験者数：2科、3科、4科

偏差値の計算には順位が必要となるため、残念ですが、私が紹介する方法では4教科の各偏差値は計算することができません。しかしながら、2科、3科、4科については、問題なく計算することができますね。

まずは、受験者と順位から、順位%を計算します。順位が高いほどゼロに近づき、順位が低いほど100に近づくように計算します。反対でも計算できますが、しばしば「上位10%」のような言い方をしますので、このほうがイメージに近いと思います。「%」と言っていますが、百分率でも0から1の小数でもどちらでも大丈夫です。

• 順位%＝順位÷受験者数

上記の式は、0～1の小数で表すことを想定し、「×100」はしていません。わかりやすいからということで百分率にしたいときには「×100」しますが、その場合、後述の関数で引用するときに「÷100」が必要となります。

偏差値の計算には、「NORM.S.INV」（エクセルのバージョンによってはピリオドが不要で「NORMSINV」）という関数を使います。「NORM.S.INV(0から1の小数表記の順位%)」という形で使います。

今回は順位が高いほど「順位%」がゼロになるように計算しています。そのため、NORM.S.INV関数で出てきた値に「-1」をかけるという操作が必要になり、そこに、偏差値の平均である「50」、偏差値の標準偏差である「10」を加味します。これにより、以下の式を導くことができます。

数式は、「順位%」が百分率になっていれば、

-1×「NORM.S.INV(“順位%")」×10＋50

または、「順位%」を0から1の小数で計算していれば、

-1×「NORM.S.INV(“順位%"/100)」×10＋50

となります。エクセルにコピペできる計算式は後述します。

「順位%」経由しなくていいんですけど・・・、という場合には、

-1×「NORM.S.INV(“順位"／"受験者数")」×10＋50

ですね。

これで、あくまでテストの点数の分布が正規分布に従うと仮定した場合ですが、順位を偏差値に換算することができます。

コピペできる計算式、エクセルシート配布、順位と偏差値の換算表

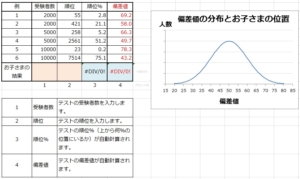
以下は、前回の記事と同じ例です。

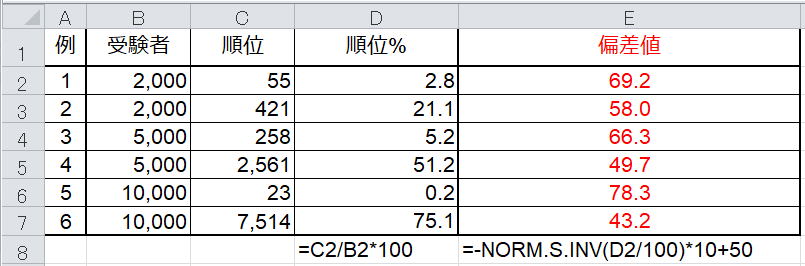
例1（2行目）の計算式は以下となっていますので、コピペして参照セルを変えればすぐに偏差値を計算できるかと思います。

受験者数（セルB2）

順位（セルC2）

順位%（セルD2）：=C2/B2*100

偏差値（セルE2）：=-NORM.S.INV(D2/100)*10+50

または、「順位%」なしで直接計算する場合には、

偏差値（セルE2）：=-NORM.S.INV(C2/B2)*10+50

実際に必要なのは、最後の赤太字の数式だけです。これで順位から偏差値を計算することができました。

計算式ではなくエクセルシートをご希望の方向けに、「日能研の育成テスト・全国テストで偏差値を計算するシート」を、以下からダウンロードできるようにしています（二次配布はどうぞご容赦ください）。

日能研の育成テスト・全国テストで偏差値を計算するシート.xlsx
（Microsoft Defenderでスキャン済みです。）
ダウンロードいただきましたら、よろしければ応援クリックいただけると励みになります！

にほんブログ村

また、エクセルにコピーすることやダウンロードすることすら面倒という方のため、上位何%にあたるかの「順位%」と「偏差値」の換算表も作成しました。

順位％	偏差値	偏差値（整数）		順位％	偏差値	偏差値（整数）		順位％	偏差値	偏差値（整数）
1	73.3	73		12	61.7	62		45	51.3	51
2	70.5	71		14	60.8	61		50	50.0	50
3	68.8	69		16	59.9	60		55	48.7	49
4	67.5	68		18	59.2	59		60	47.5	47
5	66.4	66		20	58.4	58		65	46.1	46
6	65.5	66		22	57.7	58		70	44.8	45
7	64.8	65		24	57.1	57		75	43.3	43
8	64.1	64		26	56.4	56		80	41.6	42
9	63.4	63		28	55.8	56		85	39.6	40
10	62.8	63		30	55.2	55		90	37.2	37
				35	53.9	54		95	33.6	34
				40	52.5	53

娘が通う早稲アカでは出番がなさそうですが、日能研にお通いのお子さまをお持ちで、育成テストで偏差値を計算したい、という方がいるかもと思い紹介いたしました。ご参考になれば幸いです。

参考になるブログがたくさんあります！応援よろしくお願いします！
　⇨　中学受験を目指すブログへ
　⇨　2024年受験の参考になるブログへ
　⇨　早稲アカ仲間のブログへ

Twitterで娘への日々の小さなサポートを紹介し始めました。
Follow @zeropapa_jukenTweets by zeropapa_juken

おわりに

娘が中学受験で結果を出せるかどうかはわかりませんし、今、私が考えていること、やっていることが結果につながる自信があるわけでもなく、正直なところ、試行錯誤しているのが現状です。しかしながら、私と娘は小学2年生の半ばから中学受験を意識した勉強を開始し、新4年2月からの通塾開始までに、大手塾から以下のお誘いを受けた事実があるため、低学年時の勉強についてはある程度うまく進めることができたと言ってよいのかなと思っています。

・四谷大塚の全国統一小学生テストへの決勝招待（1回）
・日能研の全国テストと学ぶチカラテストで小4からのTMクラスへの招待（3回）、および、4年生1年間の奨学生制度（授業料および教材料等全額免除）のスカラシップ資格
・早稲田アカデミーのキッズチャレンジテストおよび冬季学力診断テストで半年の授業料免除の特待（3回）

私達は幼児教育もまるで考えず、中学受験を意識したものの、経験もなく何をやればいいかわからない状態からの始まりでした。同じような状況の親御さんたちにとって、何らかの参考になればと思っていますので、応援をどうぞよろしくお願いいたします。

[linkrank]

参考までに、娘の小学1年生から3年生までの成績は、小学1年生では5回の模試の2教科で平均偏差値59.8（最低50.8）から、小学2年生では9回の平均偏差値70.3（最低62.5）、小学3年生では8回の模試の2教科で平均偏差値71.3（最低68.6）となっています。

以下は、参考記事です。

以下のリンクから「模試」カテゴリの他の記事を探せます。