【全塾共通】「あと○点取ったら偏差値△アップを調べるシミュレーター」を作ってみました
\ この学習法が娘の成績を変えました! /
中学受験に向けた偏差値アップの方法を、家庭でどう実践していくか。このテーマについて、全15章+まとめ、合計63,000字を超える圧倒的ボリュームでまとめた記事
1か月で偏差値+10を目指す!中学受験に勝つ家庭がやっている『勝ちパターン』大全
を、noteで公開しています。偏差値の上げ方に悩んでいる保護者の方にとって、きっと具体的なヒントが見つかるはずです。

偏差値と点数と順位への考え方
私が言うまでもなく、中学受験での指標の一つに、偏差値がありますね。前に受けたテストの偏差値と比べて高くなれば、私も娘もそれなりに喜びますので、気にしていないわけではないのですが、点数や順位に比べると、それほど重要視していないのが現状です。
早稲田アカデミーではカリキュラムテストと組分けテストがあります。カリキュラムテストはレベル別になってしまうので母集団が偏り、相対的に高い偏差値が取りにくくなりますので、「偏差値〇〇・・・もうダメだ」ということはないでしょう。それに比べて、組分けテストは、四谷大塚と早稲田アカデミーに通っている子どもたちがほぼすべて受けるのだと思うので、受験者数も跳ね上がり、母集団としてはかなり信頼できるようになってきます。しかしながら、四谷大塚の組分けテストには、もちろんサピックスの子たちはおりませんので、「偏差値50超えた!やった!半分より上!」というのも違うのでしょうし、「偏差値〇〇の壁を超えた!」と安心するのも楽観的と言われてしまうのかもしれません。
私がテストの結果を受けて考えるのは、「転がり落ちていかないよう、このままなるべく上の方にくらいついていくためにはどうすればよいか」です。そのため、例えば、たとえ1問しか間違っていなくても「それを理解している人がいるのだから、離されないように今のうちに理解しておこう」と考えるため、偏差値よりも点数が大事となります。復習すべき問題の優先順位付けが必要になったら、またその時考えます。そして、母集団がなんだろうが、「1位に近ければ近いほどなんだかすごそう」な気がしますし、なにより娘が喜びますので、なんだかんだで順位も励みになります。
偏差値は青天井ですし、ちょっと目標が決めにくいです。
\算数の復習、方法を間違えていませんか?/
「間違えたら解き直す」は当たり前。でも、どの問題をどう残し、どう回すかで結果は大きく変わります。
わが家が実際に取り組み、算数の偏差値を高く安定させた「解き直しノート」の全記録を、20,000字超でnoteにまとめました。
すでに累計約200人の保護者が取り入れ、算数の復習を大きく進化させています。
特別な才能は必要なく、大切なのは「仕組み」です。復習の手応えがないと感じている方は、一度のぞいてみてください。
シミュレーター作成係に任命
ここでいきなりですが、例によって、中学受験をするお子さんの割合がとても高い職場でのお話です。
ケアレスミスをしなければ・・・、問題をよく読んでいれば・・・など、「あと、〇〇点は取れた」ということをよく考えるという話がありました。
前述のとおり、私は、今は娘の内容への理解を重視しているため、間違えた問題は正答率に関わらず解き直しをして、娘にはきちんと理解できるようにしてもらっています。そのため、あまり「取れただろう点数」を考えることはないのですが、振り返ってみると、娘がいつだったかの社会カリキュラムテストで「熊本県」を「態本県」と書いたときには、「あと○○点とれたじゃん」と言ったような気がします。
「あと、〇〇点取れた」を決めれば、成績表に各点数毎の順位と偏差値が載っているので、「〇〇点取れた時の理論的な順位と偏差値」も知ることができるということです。おぉ、確かに。
でも、成績表を見つめて、あっちを見たりこっちを見たりが必要になり、大変です。そこで、「順位は無理だけど、理論偏差値はエクセルで任意に計算できるのでは?」とうっかり口をすべらせ、無事に依頼を承ることになりました。
そして、今回、誰でも使えるよう見やすく加工し(たつもり)、公開することにしました。
順位%から偏差値を計算する方法との違い
細かいところですが、念のための、過去の記事の紹介になります。
こちらは順位の%から、標準正規分布を元にして偏差値を計算する方法です。分布がわからないのが前提となっており、これしか方法がないので、このような方法をとっています。
今回は、きちんと母集団がわかっているので、標準正規分布を使う必要がありません。
一方で、標準偏差と平均点と点数は関数になっていますが、順位はそこに含まれないので、お子さまの成績から○○点とった時の理論的な順位を計算することは、残念ながらできません。点数をシミュレートして順位を知りたいのであれば、成績一覧表とのにらめっこが必要となってしまします。
平均点、お子さまの点数と偏差値を使う理由
「肝心のシミュレーターはどこ?」と思われるかもしれませんが、気になる方もいるかもしれないので、理論も記したいと思います。
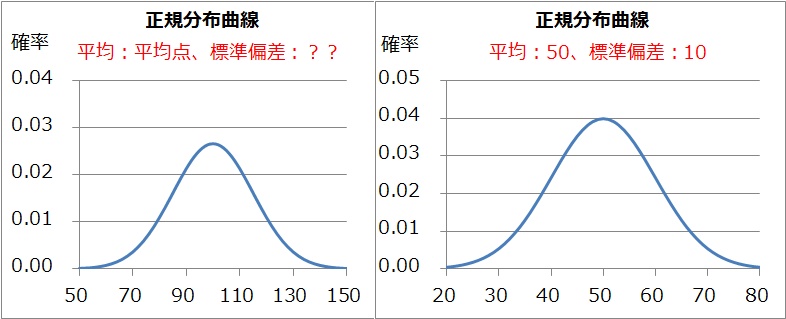
右:偏差値の分布
平均点とお子さまの点数・偏差値から標準偏差を計算できるということ
上の図は、左が点数の分布で、右が偏差値の分布です。うっかりして縦軸そろってないですが、気にしないでください。
普通、模試を受けると、点数、順位、偏差値、そして、平均点を知ることができます。しかしながら、「あと△点取ったら偏差値○アップ」を知るためには、標準偏差が必要になってしまいます。
偏差値の計算には、「テストの点数から平均点を引いて標準偏差で割る」という、統計用語で言う「標準化」という操作をします。この操作により、異なる正規分布感での比較を容易にすることができますが、この部分の計算で標準偏差が必要になるということです。
でも、私たちは、すでに子供の成績、つまり、テストの点数、偏差値、そして平均点を知っています。このため、偏差値の計算の逆算を行うことで、標準偏差を計算することができます。
正規分布の分布の形は、平均値と標準偏差で決まりますので、これで、ほぼ完全にテストの分布を特定できました。あとは、理論的な点数を入れてあげれば、理論的な偏差値を出力できるということになります。
「あと○点取ったら偏差値△アップを調べる」シミュレーター
「あと○点取ったら偏差値△アップを調べる」シミュレーターは、エクセルで作成しており、以下からダウンロードできます(二次配布はどうぞご容赦ください)。
「あと△点取ったら偏差値○アップを調べる」シミュレーター.xlsx
(Microsoft Defenderでスキャン済みです。)
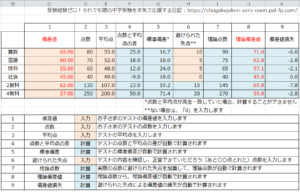
クリックで拡大します。
ファイルを開くと、上の画像のとおりのシートが開きます。
エクセルの中に説明書きも加えておりますが、入力いただくのは、背景がオレンジ色になっている、以下の4つです。入力されている数値は架空のものとなっていますので、消去してお使いください。
列番号1(C列):お子さまの偏差値
列番号2(D列):お子さまの点数
列番号3(E列):テストの平均点
列番号6(H列):避けられた失点(「あと〇〇点とれた」点数)
これらを入力すれば、列番号8(J列)に、計算された理論偏差値が出力されます。
私ならどう使うか?
勢いで作ったものの、どう使いましょうか。意味もなく「あと〇〇点とれた」を高く設定し、出力された理論偏差値を見てにやにやしても、あまり意味はないかもしれません。
まず思いつく使い方としては「計算ミス、読み間違え、転記ミスなどの、いわゆるケアレスミス分を上乗せ」することでしょう。つまり、「ケアレスミスが無ければ・・・」を想定します。
ケアレスミス防止には精神論ではなく、具体的な工夫が必要と言われていますが、私は精神論も大事だと思っています。1問の重み、1点の重みを完全に理解することなしに、ミスをゼロにすることは難しいと考えています。工夫ももちろん大事と思いますが、やはり子供をその気にさせる必要があります。
肝心なテストでミスを見つけると、ついつい「ミスで○〇点損した!」とか「ミスなくさないと入試で落ちるよ!」とかマイナス面で考えてしまいがちなのが一般的なのではないかと思いますが、「〇〇点とれれば偏差値△上がるよ!頑張ってみない??」と、励ますように、その気にさせることができるかもしれません。
もう一つは、「時間切れで解けなかった問題文を上乗せ」でしょうか。
家だとリラックスできるので塾で解けなかった問題も解けるというのはしばしばありますので、その分を上乗せしても良いかもしれません。ただし、テスト中にその問題を解くためには、その問題だけでなく、正確さを維持したまま全ての問題に対して全体的にスピードアップしなければなりません。時間切れ問題への挑戦権を得るためには、相応の努力が必要となることを考慮して上乗せする必要があると思います。
次が、一番肝心かもしれません。
考えられる上乗せ分を全部上乗せすると、それが、現時点において、子供の全力を超える力を発揮した時の成績となります。ミスも時間切れも実力であるという考えが一般的かと思いますので、ここまででもかなり楽観的な想定となっていると思います。
でも、ここまで上乗せしても目標とする成績に届かない場合、それを達成するためには、かなりの努力を要することを認識し、また、次の打ち手が必要であることを覚悟する必要がありそうです。
塾に通っている子供が多く、多少の差はあれど得られるアドバイスがほぼ同じだとすれば、親こそが、何が足りていて、何が足りていないのか、その足りていないものを解決するにはどうすればよいかを分析して、具体的な手段を実行する必要があるのだろうなと思っています。そのためにも、あらゆるパターンを想定して、日々、情報収集を続けています。
なお、低学年時にはそこまで偏差値は気にしないものだとは思いますが、私たちも、四谷大塚の全国統一小学生テスト、早稲田アカデミーのチャレンジテスト、日能研の全国テストと学ぶチカラテストを受験してきました。今回の考えは、もちろん低学年で受験する模試でもお使いいただけます。
オンラインでもできる、中学受験向けの立て直し
地方在住や送迎の都合で通塾の選択肢が限られる場合でも、オンラインで中学受験対策を進めることは可能です。
塾フォロー型の個別指導(オンライン対応)という選択肢があります。
SS-1は、中学受験専門の個別指導塾で、教室での個別指導に加え、オンライン個別指導にも対応しています。
私が調査した中で公式情報や条件を確認した限り、候補の1つとして比較対象に入れやすい印象で、資料を取り寄せておいて損はないと考えられる個別指導塾・オンライン個別指導の1つです。
SS-1では無料で資料請求ができ、指導内容や費用感を含めた具体的な情報を公式資料で確認できます。
例えば、成績が伸び悩んでいる・苦手がいつまでも苦手なまま…などの悩みが出始めているなら、個別指導を検討し始めてもよいかもしれません。
まずは資料で全体像を確認して、家庭に合う進め方を検討するのが安心です。
資料請求しておき、情報収集の第一歩として資料を読んでおくというのは、私自身が続けてきた有効な方法の1つと思っています。
迷っている段階なら、まずは資料で全体像をつかむのが早いです。
体験談も参考になりますが、私自身はまず公式資料を正しく理解することが大切だと考えています。
子どもが頑張っているからこそ、親も判断材料を集めるという形で一歩進めておくと安心です。
\ 毎月、数十人の算数の学びが大きく進化! /
中学受験算数では、間違えた問題を集めて復習・分析する「復習ノート」「解き直しノート」が有効です。
私の全記録をまとめ、魂を込めた記事(20,000字超)
中学受験・算数の成績が劇的に変わる!本気で取り組む『解き直しノート』の全記録
を、noteで公開しています。
以下のリンクからアクセスできますので、よろしければご覧になっていただければ幸いです。
Twitterで娘への日々の小さなサポートを紹介しています。
@zeropapa_juken を見る(X/Twitter)
おわりに
長女は、最終的に四谷大塚の組分け分類で新小4の通塾開始以来、最後までSコース1組(最上位コースの最上位組)を維持しました。
また、早稲アカのNNでも最初から最後まで1組を継続し、最難関校を安全校として第1志望校を受験し、無事に合格することができました。
振り返ると、私と娘は小学2年生の半ばから中学受験を意識した勉強を開始し、新4年2月からの通塾開始までに、大手塾から以下のお誘いを受けた事実があるため、低学年時の勉強についてはある程度うまく進めることができたと言ってよいのかなと思っています。
- 四谷大塚の全国統一小学生テストへの決勝招待(1回)
- 日能研の全国テストと学ぶチカラテストで小4からのTMクラスへの招待(3回)、および4年生1年間の奨学生制度(授業料・教材費等全額免除)
- 早稲田アカデミーのキッズチャレンジテストおよび冬季学力診断テストで半年の授業料免除の特待(3回)
私達は幼児教育もまるで考えず、中学受験を意識したものの、私には中学受験どころか人生で受験した経験もなく、何をやればいいかわからない状態からの始まりでした。
同じような状況の親御さんたちにとって、何らかの参考になればと思っていますので、応援をどうぞよろしくお願いいたします。
参考までに、娘の小学1年生から3年生までの成績は、
・小学1年生では5回の模試の2教科で平均偏差値59.8(最低50.8)、
・小学2年生では9回の平均偏差値70.3(最低62.5)、
・小学3年生では8回の模試の2教科で平均偏差値71.3(最低68.6)
・小学6年生の合不合判定テストでは4科偏差値76、NNオープン・SAPIXオープンもすべて合格率80%、通算で全統小決勝進出・成績優秀者5回、中学受験は全勝+最難関校に無事進学
という結果でした。
以下は、参考記事です。









